The Buckblog

Once you start playing with mazes, you soon discover that there are a lot of different ways to draw them. The easiest way is what I call a linewise rendering, and it looks something like this:

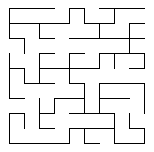
The path to follow is the line itself, and whitespace becomes the walls. Straightforward to implement, but honestly, it’s not the most friendly of representations. For one thing, because the paths have no thickness, it becomes difficult to represent the contents of the maze: doors, stairs, obstacles, etc.

To add thickness to the paths, you can render what I call linewise walls. The following illustrates the same maze as before, but with linewise walls:

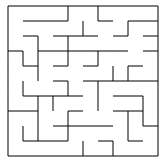
This flips it around, making the lines the walls, and the whitespace the actual passages of the maze. Now it’s easier to draw on the cells themselves. (This happens to be the technique I use in my book, since it is my go-to representation for mazes. It’s really a flexible way to do it.)

However, every once in a while I get asked how to render a maze where the walls have actual thickness. (This is often in the context of someone wanting to build a maze in a game like Minecraft.) I call this kind of representation a blockwise rendering, because the simplest way to do it is to draw everything as blocks. Again, the same maze as before, this time drawn with blockwise geometry:

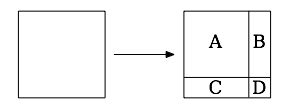
It’s not hard at all to draw a maze in this style. For every cell in your grid, you just divide it into quarters, like this:

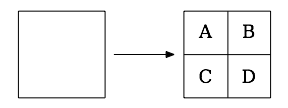
The northwest subcell (A) will always be a passage, and the southeast subcell (D) will always be a wall. Then, depending on whether the cell has a connection to the south and east cells, the southwest (C) and northeast (B) subcells will either be walls or passages, as follows:

1. If the original cell is linked to its southern neighbor, make the southwest subcell (C) a passage; otherwise, make it a wall.
2. If the original cell is linked to its eastern neighbor, make the northeast subcell (B) a passage; otherwise, make it a wall.

Then, because we’re only considering south and east passages, we need to treat the north and west boundaries of the maze specially, by rendering them explicitly as a wall. The result of all this is that if you start with a grid that is n cells on a side, the blockwise rendering will be 2n+1 blocks on a side: 2n because you double each cell, and +1 because of the extra wall on the north and west boundaries.

But is it still the same maze?

Note that the maze remains exactly the same, topologically. Blockwise or linewise, it doesn’t matter how you render it. Consider the following demonstration. All three mazes below are exactly the same, but the one on the left is rendered linewise, the one in the middle has linewise walls, and the one on the right is rendered blockwise:

(Click or tap any of the renderings to generate another maze.)

Can I generate a blockwise maze directly?

My book describes representing a maze as, essentially, a graph–with cells for nodes and passages for edges. This maps directly to linewise renderings, and easily converts to linewise walls. You’ve seen, now, how to convert those to blockwise renderings, but what if you only care about the blockwise representation? Perhaps you want the walls themselves to have attributes (color, texture, hardness, etc.), or maybe you want players to be able to tunnel through walls, in which case they need to be entities in their own right.

Is it possible to skip the intermediate graph representation, and just build the maze directly in a blockwise format?

Absolutely!

You have two options. I call these strict blockwise, and relaxed blockwise.

Strict Blockwise Mazes

A strict blockwise representation can be converted back into linewise and linewise-wall renderings by throwing away the north and west walls, and then laying converting each 2x2 group of blocks back into lines, based on how they connect to neighboring 2x2 groups.

To generate a strict blockwise maze, the grid must have an odd number of rows and columns, and you’re going to treat only blocks at odd-numbered rows and columns as actual cells, like this:

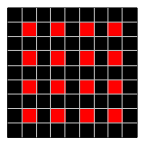
The remaining cells are intermediate locations, which are used only to represent passages between cells. The process of generating a maze progresses using your algorithm of choice, with passages being carved through those intermediate locations.

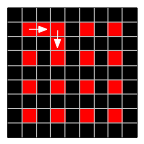
Just like that.

Relaxed Blockwise Mazes

A relaxed blockwise representation cannot usually be converted back into a linewise rendering. This is because it treats every block in the grid as a potential cell in the maze, which means you can no longer reliably overlay a larger grid on it and reduce those 2x2 clusters to single cells.

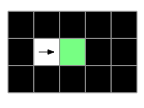
To generate a relaxed blockwise maze, start with a grid of any size you like, and the algorithm of your choice. Proceed as before, but now you are constrained in which neighbor cells you can choose: if a neighbor cell is horizontally or vertically adjacent to any other “open” (carved) cell (aside from the current cell), it may not be selected.

In the following illustration, the green cell may be carved from the west because it has no neighboring cells that are themselves already carved (aside from its neighbor to the west).

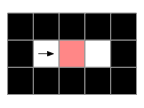
But in the next illustration, the red cell may not be carved from the west, because it does have a neighboring cell that is already carved (its neighbor to the east).

Following these rules generates mazes like this:

(Tap the maze to generate another one.)

Note that you’ll often wind up with “dead” cells–groups of wall that couldn’t be carved because they violate that constraint about which cells can be selected. Sometimes that’s an esthetic that you want; sometimes it isn’t. It’s something to keep in mind.

Do the walls have to be the same size as the cells?

Definitely not! This post is getting much longer than I intended, though, so I’ll leave this one as an exercise for the reader. Here’s a hint, though: remember how we divided the cells into quarters? Think about what would happen if you divided them into unequal quarters, like this:

See what happens!

So, there you have it: mazes with blockwise geometry. You are now ready to create your own Roguelike dungeon. Go forth and carve some passages!