The Buckblog

This morning as I was getting ready for the day, I was thinking about the Recursive Division algorithm. (Maze algorithms are on my mind a lot these days.)

It’s a neat algorithm, with some neat properties (like the ability to generate different sized “rooms” in a maze by controlling the depth of the recursion), but it suffers from at least one crippling flaw: glaringly obvious bottlenecks.

Bottlenecks are passages in a maze that effectively divide a maze into two distinct regions. In order to move from one region to another, the player has to pass through that passage. All mazes have them (because that’s a property of perfect mazes, or spanning trees), but in mazes generated by this algorithm, the bottlenecks are really easy to spot. And that’s a bad thing, because it means that a player can generally identify a solution by finding the bottlenecks and working backward to a solution.

Here’s an example of a bottleneck in a maze generated by recursive division:

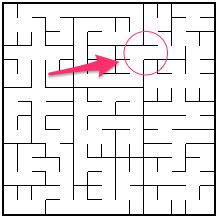
You can easily see how the passage highlighted in that image takes you between two distinct regions of the maze, one on the west and one on the east, and the only way to move between them is via that passage.

That feature alone is enough to scare me away from the recursive division algorithm, but I got to wondering: what if it were possible to do recursive division using an irregular line to divide the regions? Instead of a straight wall moving from one side of the maze to the other, obviously separating the grid in half, you’d have divisions formed by meandering walls, much more natural and harder to spot.

So I hit on the following algorithm. It’s not really anything new—just recursive subdivision with a different rule for splitting regions in half—but the results are much more promising.

1. Collect all the cells in the maze into a single region.

2. Split the region into two, using the following process:

   1. Choose two cells from the region at random as “seeds”. Identify one as subregion A and one as subregion B. Put them into a set S.
   2. Choose a cell at random from S. Remove it from the set.
   3. For each of that cell’s neighbors, if the neighbor is not already associated with a subregion, add it to S, and associate it with the same subregion as the cell itself.
   4. Repeat 2.2 and 2.3 until the entire region has been split into two.

3. Construct a wall between the two regions by identifying cells in one region that have neighbors in the other region. Leave a gap by omitting the wall from one such cell pair.

4. Repeat 2 and 3 for each subregion, recursively.

It came together really well, which is kind of a first for me. I usually have these ideas that sound wonderful in the shower, and then turn out to have all kinds of gotchas hidden in the assumptions. (Remind me to tell you about my idea to generate unicursal mazes from scratch, sometime.)

Here’s an example of a maze being generated using this technique. We start with an empty 10x10 space:

We plant two seeds and let them grow to fill the entire region, and then draw a wall between them, making sure to leave a gap in the wall.

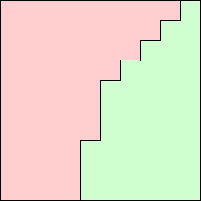
Then we repeat that for each side. Following one side of the recursion down, we get the following sequence of divisions:

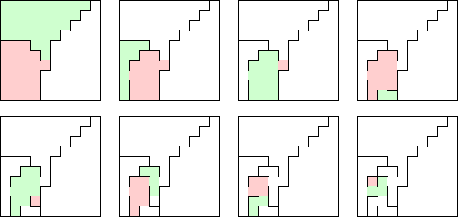
The algorithm would, of course, repeat on every region until the regions are smaller than some threshold. The smallest threshold would be 1–a region consisting of a single cell, but in practice the smallest threshold is actually 4 because while you can divide a region of two or three cells into two distinct regions, you cannot then separate them with a wall and keep them connected.

The final maze looks like this:

Quite a bit nicer than the vanilla recursive subdivision maze! The bottlenecks are less glaringly obvious, which alone is a big win. But check this out:

What we have here is a 50x50 maze generated using this “blobby” recursive division variant, but the recursion stops when a region contains fewer than 20 cells. The bottlenecks are all but invisible here, resulting in a surprisingly challenging maze! Further, while such “rooms” generated using a standard recursive division algorithm would all be rectangular, we get much more organically-shaped rooms with this variant.

Another benefit of this variant is that it works out really well for any kind of grid topology, because walls simply follow the boundaries of cell regions.

It’s particularly fun to watch in action. I’ve put together a few different sized grids that you can run the algorithm on, below. Click “run” to have the algorithm run to completion, or press “step” to move through the process incrementally.

Room size: None (corridors only) Small Medium Large

It strikes me just now, watching that last demo run, that this could also be used to draw random maps. Especially with the “room size” set to “huge”, the grid in the bottom right looks remarkably like a map of counties!

Anyway, I need to get back to work on my book, but I just wanted to share this little discovery. It certainly made me smile this morning!